College Algebra Homework 06
Description (10 points) Selected solutions from Assignments 16 and 17, 3.3–3.4.
The following is a listing of the assigned problems for Homework 06.
| # | Section | Page | Exercises |
| 16 | 3.3 | 205 | 13,14,17,18,21–28,31–34,35,37–40,46,55,56;61–66;67,68 |
| 17 | 3.4 | 213 | 3,6,8,11,12,13 |
The graded problems with solutions follow.
§3.3 Quadratic Equations
Throughout the assignment, I’ll use the letter S to denote the solutions set.
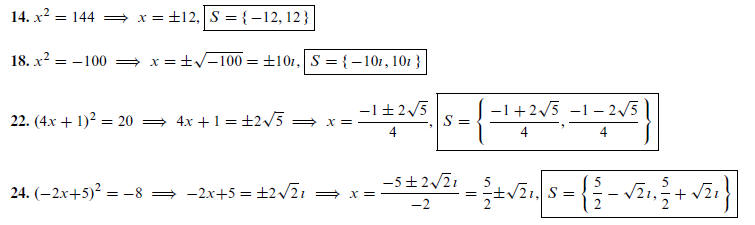
32. −5 + 16x − 3x^2 = 0, we’ll use the Quadratic Formula to solve.
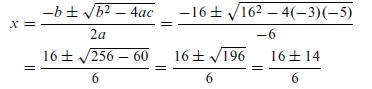
Thus,…
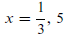
The solution set is S = {1/3, 5 } .
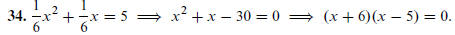
The solution set is S = {−6, 5 }
40. 9x^2 − 12x + 8 = 0, we use the Quadratic Formula:
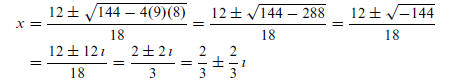
The solution set is
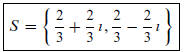
46. Solve x^2 − 2x + 5 = 0. We use the Quadratic Formula:
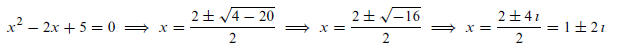
The solution set is S = { 1 − 2ı, 1 + 2ı }
62. The discriminant is D = b^2−4ac = 100 > 0. Since D >0,
there are two real solutions and since the discriminant
is a perfect square, we see that the solutions are rational numbers.
64. The discriminant is D = 8 > 0. Since D > 0, there are
two real solutions and since discriminant is not a perfect
square, we see that the solutions are irrational numbers.
68. The discriminant is D = −44 < 0. Since D <0, there are no real solutions, but there are two complex solutions
68. Construct the polynomial (x + 3)(x − 2) = 0 ⇒ x^2 + x
− 6 = 0. So, to answer the question: a = 1, b = 1,
c = −6
§3.4 Applications
3. Sum of two numbers. The sum of two positive numbers is 30, let x denote one of the two numbers.
(a) The other number is 30 − x
(b) The restrictions on x are 0 < x < 30.
(c) The product function is P(x) = x(30 − x) = 30x − x^2
(d) Maximize the product.
Solution: We note that P(x) is a polynomial of degree two,
the coefficient of x^2 is negative, that implies the
parabola opens downward and the vertex is a maximum. We simply find the
coordinates of the vertex using
the infamous Vertex Formula:
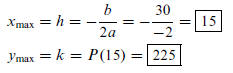
Summary: The two numbers are 15 and 15, their product is 225.
6. This problem was done is class. See your notes.
8. Volume of Box. See statement of problem on page 214.
(a) What is the length of the other side of the sheet metal 2.5x
(b) What are the restrictions on x: x > 6
(c) Determine the volume function:
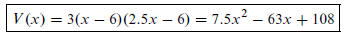
I didn’t grade the following problems, but will supply the solutions for comparison with your solutions.
11. A square has an area of 800 square feet, and a
sprinkler is placed in the center, what is the radius of the sprinkler.
Well, it seems to me that radius will be half the diagonal of the square. Let s
denote the length of the side of the
square, then s^2 = 800
The diagonal is the hypotenuse of the triangle whose other two sides are 800
each.
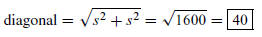
The radius is half the diagonal, so the radius of the sprinkler is 20 feet
12. From the diagram we have (x − 10)^2 + x^2 = 50^2.
Expanding and combining, we get, 2x^2 − 20x − 2400 = 0,
dividing by 2 we get x^2 − 10x + 1200 = 0. I see we can factor (x − 40)(x + 30)
= 0. We see x = 40 and
x = −30. The second solution does not make sense in this applied problem.
Therefore, the answer is x = 40 feet
13. Similar to Problem #12. We solve the equation (2h + 3)^2 = h^2 + 12^2 for h. We have 3h^2 + 12h − 135 = 0
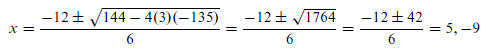
Throwing out the negative value, we see that h = 5 ft


