College Algebra Review
The first test (Test #1) will occur on Wednesday, October 1, 2008 and will
cover the following
sections of the text:
§1.1-1.6,§7.1, and
§2.1-
2.6. Below are my comments on
each of these
sections.
It goes without saying—but not without writing—that it is assumed that you have
had a good and
honest attempt at the assigned exercises. Pay attention to these problem types,
especially the ones
that I deemed important enough to grade.
Chapter 1: Linear Functions, Equations, and Inequalities
§1.1 Real Numbers and the Rectangular Coordinate System. This section
contains some
basic terminology concerning natural number, whole numbers, rational numbers,
irrational
numbers, and real numbers. These are all terms you’ve studied before and should
know. Knowledge of these number systems is assumed, and will not be explicitly
tested
over. Similarly, it is assumed you know the rectangular coordinate system,
plotting and
graphing will occur on this test; know such terms as Quadrant I–Quadrant IV.
There are three important formulas in this section that you will be tested on:
Pythagorean
Theorem, the Distance Formula, and the Midpoint Formula.
§1.2 Introduction to Relations and Functions. You should know the
interval notation, and
the set-builder notation. An example of each follows:
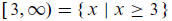
A relation is a set of ordered pairs. A relation has a domain and
range. A function
is a special kind of relation. You should be able to work with simple discrete
relations
and functions. Relations have graphs, and you should be able to work with the
graph of
a relation, identifying its domain and range. The Vertical Line Test is a visual
way of
discerning if a relation is a function.
The function notation is of supreme important. A common with of defining a
function f
is through this notation. For example, f (x) = 2x2 − 1 uses an algebraic
expression to
define the function. The variable x is the independent variable (an element in
the domain
of the function). We use this notation as follows: if we wish to find the value
of this
function at x = −2, then f (−2) = 2(−2)2 − 1 = 2(4) − 1 = 7.
§1.3 Linear Functions. A linear function has the form f (x) = ax +
b, where a and b are
numbers. Its graph is a line. As we progressed through this section, we learned
that a
and b had certain (geometric) meanings:
• The number a turned out to be the slope, m, of the line.
• The number b is the y-intercept of the line.
Slope of a Line. Given two points (x1, y1) and (x2, y2), the slope of the line
passing
through these two points is given by
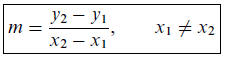 (1)
(1)
You should know this formula, and how to use it. The sign of m give important
information
about the slant of the line, see page 30 on the Geometric Orientation Based on
Slope.
The slope-intercept form of the equation of a line. Given the slope m and the
y-intercept,
b, of a line, the linear function describing this line is given by
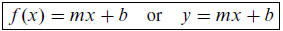 (2)
(2)
Know this form, and the interpretation of its parameters (m and b), for
example, the
equation y = 2x − 3 is the equation of a line with slope m = 3 and y-intercept
of
b = −3.
§1.4 Equations of Lines and Linear Models. In this section we looked at
several formulas
for developing the equation of a line, notions of parallel and perpendicular
lines were
introduced, and a brief discussion of linear regression was presented.
Point-Slope Form. Given a point (x1, y1) and a slope m,
the equation of the line passing
through the point and having the given slope is
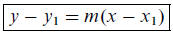 (3)
(3)
This is a transitional form, normally, we set up the equation using the
point-slope form,
then convert it into one of the others, most notably, the slope-intercept form
(2), or the
standard form (4). You should know how to use this formula, most certainly, and
how to
convert it to the slope-intercept form
Standard Form. The standard form for an equation of a line is of the form
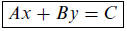 (4)
(4)
Be able to convert an equation in standard form to the slope-intercept form;
for example,
2x−3y = −1 converts to 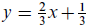 . Thus, 2x−3y = −1 is a
line with slope m = 2/3
. Thus, 2x−3y = −1 is a
line with slope m = 2/3
and crosses the y-axis at y = 1/3.
Parallel Lines. Two lines are parallel if they have the same slope.
Example 4, page 39,
is an important type of problem.
Perpendicular Lines. Two lines are parallel if their slopes have a
product of −1. Example
5, page 41, is an important type of problem. Note that if the slopes of the
perpendicular
lines are m1 and m2, then m1m2 = −1, or m2 = −1/m1, this latter formula is
useful if
you wish to compute the slope of any line perpendicular to a given line.
Linear Models and Regression. We discussed this topic in class and had a
homework
set over regression. We’ll not cover this on the test itself.
§1.5 Linear Equations and Inequalities. A linear equation is one of the
form ax +b = c, or
any equation that reduces to that form. You have been solving such equations
since 8th,
just continue as you did in the past, only without error.
There is some discussion about the graphical interpretation of intersecting
graphs; I doubt
if that will be explicitly on the exam, but you should be able to analytically
find the
intersection point; for example, where do the two lines y = 4x − 1 and y = 2x +
1
intersect? We begin by setting the y-values equal:
| 4x − 1 = 2x + 1 | Set the functions equal |
| 2x = 2 | Subtract 2x and add 1 to both sides |
| x = 1 | divide ! |
However, when x = 1, y = 4(1) − 1 = 3. The two lines intersect at the point
(1, 3)
Linear inequalities are also covered. Their solution is typically in interval.
Standard
algebraic tricks work except for dividing or multiplying both sides by a
negative number,
in this case the inequality is reversed.
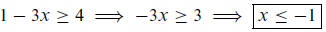
The solution set is then (−∞,−1 ] . Actual inequalities seen on the test my
be more line
Example 6, p. 58, where some additional routine algebra is needed.
§1.6 Applications to Linear Functions. We covered Applications to
Linear Equations,
(simple geometric problems, mixture problems) and Break Even Analysis.
Expect problems
of the type that were on the homework.
Chapter 7: Systems of Equations
§7.1 Systems of Equations. We popped into this section to pick up the
techniques for solving
a system of linear equations:
ax + by = c
dx + ey = f
Such a system has one of three possible solutions: (1) a unique solution; (2) no
solution,
or the empty solution ; or (3) infinitely many solutions.
There are two techniques for solving such a system: (1) the substitution
method; (2) the
elimination method.
The Substitution Method is the one you should be most familiar with. Here
you solve
for one variable in one of the two equations, and substitute it into the other
equation.
The Elimination Method. The idea behind the elimination method is to
eliminate one
of the two variables, and solve for the remaining variables. We do this by
matching the
coefficients of the variable we want to eliminate. For example:
| 5x + 7y = 6 | (1) | |
| 10x − 3y = 46 | (2) | |
| −10x − 14y = −12 | (3) | multiply (1) by −2 |
| −17y = 34 | add (2) and (3) | |
| y = −2 | (4) | solve |
| 5x + 7(−2) = 6 | Subst. (4) into (1) | |
| x = 4 | (5) | …and solve for x |
From (4) and (5), the solution set is { (4,−2) } .
We studied only linear systems—not the nonlinear systems—and the exercises
reflected
that.
Chapter 2: Linear Functions, Equations, and Inequalities
§2.1 Graphs of Basic Functions, Symmetry. You need to have a basic
understanding of
continuity (at least, be able to pick one of the crowd). By looking at a graph,
you should
be able to determine where it increases and decreases.
The following functions are basic, you should know there graphs, and able to
answer
questions on continuity, increasing, decreasing, domain, and range. You need to
know
what the graphs of these basic functions look like:
• The identify function f (x) = x
• The squaring function f (x) = x2. Its graph is a parabola, and is symmetric
with
respect to the y-axis:
f (−x) = f (x) Criterion for y-Axis Symmetry
• The cubing function f (x) = x3. Its graph is symmetric with respect to the
origin:
f (−x) = −f (x) Criterion for Origin Symmetry
• The square root and cube root functions f (x) =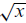 and
f (x) =
and
f (x) =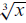 .
.
• The absolute value function f (x) = |x|
• The x = y2 relation and x-Axis symmetry
An even function is just one that has y-axis
symmetry, while an odd function is one
with origin symmetry.
§2.2 Vertical and Horizontal Shifting of Graphs. Geometrically easy to
understand. Know
this material.
§2.3 Stretching, Shrinking, and Reflecting Stretching and shrinking are a
little trickier to
understand graphically. Not much emphasis will be placed on this section except
for
reflecting. We reflect a graph y = f (x) across the x-axis by graphing the
function
y = −f (x), and we reflect a graph with respect to the y axis by graphing the
function
y = f (−x).
§2.4 Absolute Value Functions: Graphs, Equations, Inequalities. Consider
the function
y = f (x), and define y = |f (x)|. There is a definite relation between these
two graphs.
This is an important point.
The other content of this section concerns solving equations and inequalities
that involve
absolute values. Some simple exercises will appear on the exam.
§2.5 Piecewise-Defined Functions. Be ready to graph and calculate the
values of a piecewise defined
function. The greatest integer function, p. 141, will not be covered.
§2.6 Operations and Compositions. The simple arithmetic operations were
briefly discussed
(p. 149), a greater emphasis was placed on composition of functions, p.
152. Examples 5,
6, and 7 are of particular importance.
That was a lot of (review) material!! Hope we can slow the
pace as we progress through the book.
The test, no doubt, will have some short answers (true/false, fill in the blank)
and some questions
involving computation, algebra and graphing. Good luck, but more importantly,
good knowledge.
I shall attempt to construct a fair test over these topics.


