Review of Matrix Algebra
RANK OF A MATRIX: The rank of a matrix is the maximum
number of linearly independent columns
that may be selected from the columns of the matrix. It is sort of a measure of
the extent of "duplication
of information" in the matrix. The rank of a matrix may be equivalently defined
as the number of linearly
independent rows (by turning the matrix on its side). The rank determined either
way is the same.
Thus, the largest that the rank of a matrix can be is the minimum of r and c.
The smallest rank may
be is 1, in which case there is one column such that all other columns are
direct multiples.
In the above, the rank of the matrix A is 2. To see this, eliminate one of the
columns (we have already
seen that the three columns are linearly dependent, so we can get the third from
the other two). Now
try to find a new linear combination of the remaining columns that has some
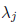not equal to 0. If this
can not be done - stop and declare the rank to be the number of remaining
columns.
FULL RANK: A matrix is said to be of full rank if its rank is equal to the minimum of r and c.
FACT: If X is a (r × c) matrix with rank k, then X'X also
has rank k. Note, of course, that X'X is
a square matrix of dimension (c × c). If k = c, then X'X is of full rank.
INVERSE OF A MATRIX: This is related to the matrix version
of "division" - the inverse of a matrix
may be thought of in way similar to a "reciprocal" in the world of real numbers.
• The notion of an inverse is only defined for square matrices, for reasons that will be clear below.
• The inverse of the square matrix A is denoted by A-1
and is the square matrix satisfying
AA-1 = I = A-1A
where I is an identity matrix of the same dimension.
• We sometimes write Ik when I is (k × k) when it is important to note explicitly the dimension.
Thus, the inverse of a matrix is like the analog of the
reciprocal for scalars. Recall that if b is a scalar
and b = 0, then the reciprocal of b, 1/b does not exist { it is not defined in
this case. Similarly, there
are matrices that "act like zero" for which no inverse is defined. Consequently,
inverse is only defined
when it exists.
Computing the inverse of a matrix is best done on a
computer, where the intricate formulae for matrices
of general dimension are usually built in to software packages. Only in simple
cases is an analytic
expression obtained easily (see the next page).
A technical condition that an inverse of the matrix A
exist is that the columns of A are linearly
independent. This is related to the following.
DETERMINANT: When is a matrix "like zero?" The determinant
of a square matrix is a scalar
number that in some sense summarizes how "zero-like" a matrix is.
The determinant of a (2 × 2) matrix is defined as follows.
Let
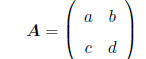
Then the determinant of A is given by
|A| = ad - bc.
The notation |A| means "determinant of," this may also be
written as det(A). Determinant is also
defined for larger matrices, although the calculations become tedious (but are
usually part of any decent
software package).
The inverse of a matrix is related to the determinant. In
the special case of a (2 × 2) matrix like A
above, it may be shown that
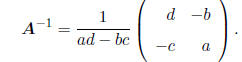
Inverse for matrices of larger dimension is also defined
in terms of the determinant, but the expressions
are complicated.
GENERAL FACTS:
• If a square matrix is not of full rank, then it will
have determinant equal to 0. For example, for
the (2 × 2) matrix above, suppose that the columns are linearly dependent with a
= 2b and
c = 2d. Then note that
|A| = ad - bc = 2bd - 2bd = 0:
• Thus, note that if a matrix is not of full rank, its
inverse does not exist. In the case of a (2 × 2)
matrix, note that the inverse formula requires division by (ad-bc), which would
be equal to zero.
EXAMPLE:
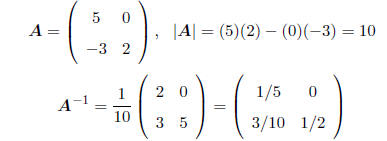3
5
Verify that AA-1 = A-1A = I.
ADDITIONAL FACTS: Let A and B be square matrices of the same dimension whose inverses exist.
• (AB)-1 = B-1A-1, (A-1)' = (A')-1:
• If A is a diagonal matrix, that is, a matrix that has
non-zero elements only on its diagonal,
with 0's everywhere else, then its inverse is nothing more than a diagonal
matrix whose diagonal
elements are the reciprocals of the original diagonal elements, e.g., if
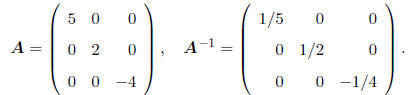
Note that an identity matrix is just a diagonal matrix whose inverse is itself, just as 1/1=1.
• |A| = |A'|
• If each element of a row or column of A is zero, then |A| = 0.
• If A has any rows or columns identical, then |A| = 0.
• |A| = 1/|A-1|
• |AB| =|A||B|
• If b is a scalar, then
,
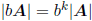where k is the dimension of A.
• (A + B)-1 = A-1 - A-1(A-1 + B-1)-1A-1
• If A is a diagonal matrix, then |A| is equal to the product of the diagonal
elements, i.e.
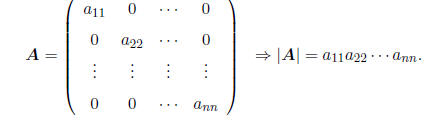
USE OF INVERSE { SOLVING SIMULTANEOUS EQUATIONS: Suppose
we have a set of simultaneous
equations with unknown values x, y, and z, e.g.
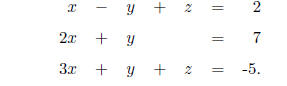
We may write this system succinctly in matrix notation as
Aa = b, where
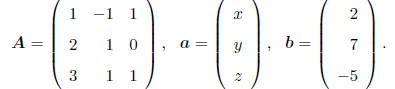
Then, provided A-1 exists, we may write the solution as
a = A-1b.
Note that if b = 0, then the above shows that if A has an
inverse, then it must be that a = 0. More
formally, a square matrix A is said to be nonsingular if Aa = 0 implies a = 0.
Otherwise, the matrix
is said to be singular.
Equivalently, a square matrix is nonsingular if it is of full rank.
For a square matrix A, the following are equivalent:
• A is nonsingular
• |A| ≠ 0
• A-1 exists
We will see that matrix notation is incredibly useful for
summarizing models and methods for longitudinal
data. As is true more generally in statistics, the concepts of rank and
singularity are very important.
Matrices in statistical models that are singular generally reflect a problem {
most often, they reflect
that there is not sufficient information available to learn about certain
aspects of the model. We will
see this in action later in the course.
EXAMPLE: Returning to the matrix representation of the
simple linear regression model, it is possible
to use these operations to streamline the statement of how to calculate the
least squares estimators of
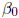and
.
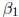Recall that the least squares estimators
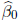and
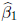for the intercept and slope minimize the
sum of squared deviations
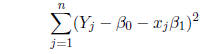
and are given by
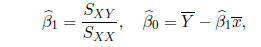
where
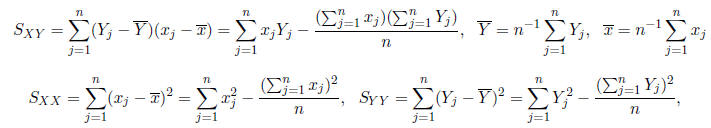
We may summarize these calculations succinctly in matrix
notation: the sum of squared deviations may
be written as
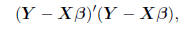
and, letting
,
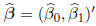the least squares estimator for β may be written
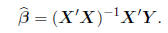
Verify that, with X and Y defined as in (2.1), this matrix equation gives the usual estimators above.
CONVENTION: Here, we have referred to
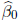and
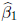as estimators, and have written them in terms of
the random variables Yj . The term estimator refers to the generic function of
random variables one
would use to learn about parameters like
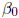or
.
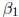The term estimate refers to the actual numerical
values obtained by applying the estimator to data, e.g., y1,...., yn in
this case.
We will see later that matrix notation is more generally
useful for summarizing models for longitudinal
data and the calculations required to fit them, the simple linear regression
model above is a simple
example.
TRACE OF A MATRIX: Defining this quantity allows a
streamlined representation of many complex
calculations. If A is a (k × k) square matrix, then define the trace of A, tr(A),
to be the sum of the
diagonal elements, i.e.
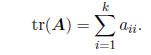
If A and B are both square with dimension k, then
• tr(A) = tr(A'), tr(bA) = btr(A)
• tr(A + B) = tr(A) + tr(B), tr(AB) = tr(BA)
QUADRATIC FORMS: The following form arises quite often.
Suppose A is a square, symmetric
matrix of dimension k, and x is a (k × 1) column vector. Then
x'Ax
is called a quadratic form. It may be shown that
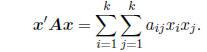
Note that this sum will involve both squared terms
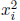and cross-product terms xixj , which forms
the basis for the name quadratic.
A quadratic form thus takes on scalar values. Depending on
the value, the quadratic form and the
matrix A may be classified. With x ≠ 0,
• If x'Ax ≥ 0, the quadratic form and the matrix A are
said to be nonnegative definite
• If x'Ax > 0, the quadratic form and the matrix A are said to be positive
definite. If A is
positive definite, then it is symmetric and nonsingular (so its inverse exists).
EXAMPLE: The sum of squared deviations that is minimized
to obtain the least squares estimators in
regression is a quadratic form with A = I,
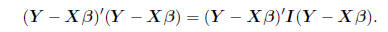
Note that this is strictly greater than 0 by definition,
because it equals
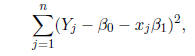
which is a sum of squared quantities, all of which must be positive (assuming
that not all deviations
are identically equal to zero, in which case the problem is rather nonsensical).
FACT: x'Ax = tr(Axx'), this may be verified by simply
multiplying out each side. (Try it for the sum
of squared deviations above.)