Linear Algebra

Vectors

k-vector as point in Euclidean k dimensional space (R^k)

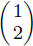  is a point in R².

Note that for reasons to clear later, we always represent vectors as COLUMN vectors
Define addition of to two vectors as the sum element by element, so

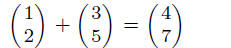(1)

where addition is only defined for two vectors in same dimensional space (so both must be
k-vectors)
Define scalar multiplication as the element by element product of the scalar with each
element of the vector

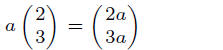(2)

Linear combination of vectors x and y is ax + by for any scalars a and b.
Consider a set of vectors. The span of this set is all the linear combinations of the vectors.
Thus the span of {x, y, z} is the set of all vectors of the from ax + by + cz for all scalars
(real numbers) a, b, c.

Basis, dimension

Consider a set of vectors, X. Suppose X is the span of some vectors a₁, . . . a_n. The latter
set is a basis for X.

There are lots of bases for X. Often one has really nice features and so we use it.
Particularly interested in basis of Rⁿ. Consider R². A nice basis is the two vectors
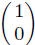
and

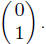
Note that any vector in R², say 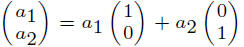so we have a basis.
But lot of others, say 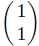and 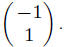Need to show that

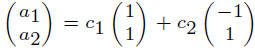  for some scalars c₁ and c₂.

To see we can do this, just solve the two linear equations. Note that vectors and solving
linear equations intimately related.

Note that if {x, y} is a basis, so is {x, y, z} for any z since we can just write
a = a₁x + a₂y + 0z since {x, y} is a basis.

A set of vectors is linearly dependent if there is some non-trivial linear combination of the
vectors that is zero. By non-trivial we mean a combination other than with all scalars being
zero, since 0x + 0y = 0 of course.

A set of vectors is linearly independent if it is not linearly dependent.

Note that is a set of vectors is linearly dependent, we have, say, ax + by = 0 for non-zero a
or b, so we can write 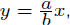that is, one vector is a linear combination of other vectors in
the set.

Since we can always rewrite a vector that is a linear combination of a linearly dependent set
of vectors as a new linear combination of the linearly independent subset of the vectors. Thus
we can say a nice basis consists only of linearly independent vectors.

We also particularly like the “natural” basis of 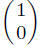and 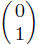where each vector is of unit
length and the two are orthogonal (at right angles). But, as noted, tons of other bases, even
if restrict to linear dependence. Let us call the vectors in the natural basis i₁, i₂ and
similarly for higher dimensional spaces.

Note that two vectors form a basis for R², and 2 is the dimension of R². This is not an
accident, the dimension of a vector space is the number of linearly independent vectors
needed to span it.

Note also that in R² that any three vectors must be linearly dependent, since we can write
the third vector as a linear combination of the other two.
Again, just solve the equations to make the third vectors sum to zero non-trivially.
Note that any set of vectors that include the zero vector 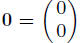must be linearly
dependent since, say, 0x + a0 = 0 for a ≠ 0.

Matrices

A matrix is a rectangular array of numbers or a series of vectors placed next to each other.
An example is

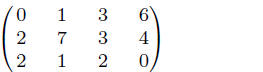(3)

Matrices are called m × n with m rows and n columns.

We can define scalar multiplication in the same way as for vector, just multiply each element
of the matrix by the scalar.

We can define addition of matrices as element by element addition, though we can only add
matrices of the same number and rows and column.

Can understand matrices by the following circuitous route:

A linear transform is a special type of transformation of vectors; these transforms map n
dimensional vectors into m dimensional vectors, where the dimensions might or might not be
equal.

A linear transform, T has the properties:

T(ax) = aT(x)where ais a scalar   (4)
T(x + y) = T(x) + T(y)   (5)

Note that if we know what T does to the basis vector, we completely know T since

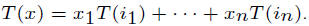
Let us then think of an m × n matrix as defining a linear transform from Rⁿ to R^m where
the first column of the matrix tells what happens to the i₁, the second column to i₂ and so
forth.

Thus the above example matrix defines a transform that takes i₁ to the vector and so
forth.

Thus we can define Mx, the product of a matrix and a vector as the vector that the
transform defined by M maps x into.
Say 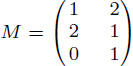  which is a linear transform from R² → R³. What happens to, say

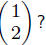  This vector is 1i₁ + 2i₂ and so

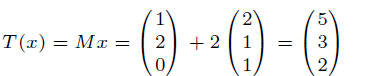(6)

This is the same thing we do woodenheadly by taking each element by taking the sum of the
product of the elements of row i with the vector.

We could compute MN by thinking of N as a k column vectors, and the above operation
would produce k column vectors with the same number of rows as M. Note that the number
of columns in M (the dimension of the space we are mapping) from must equal the number
of elements in each of the column vectors of N.

But we can also think of the matrix product MN as the composition of the transforms
corresponding to M and N. Say M is n × m and N is m × k.

So N takes k vectors into m vectors and M takes m into n vectors so we can see MN
takes k vectors into n vectors, by first taking them into m vectors and then taking those m
vectors into n vectors.

To understand the resulting product in matrix form, just think of it as telling us what
happens to the k basis vectors after the two transformations. It is easy to see that the i, jth
element of the product is given to us by taking the sum of the element by element products
of row i and column j, and that we can only multiply matrices where the number of columns
in the first one equals the number of rows in the second.

Note that matrix multiplication is not commutative, in that NM will usually not even be
defined, since M takes m vectors into n vectors but N takes k vectors into m vectors, so
N cannot operate on the vectors produced by M.

We can also think of M + N as corresponding to the transform which has
M + N(x) = M(x) + N(x), always assuming the matrices are of the right dimension (in
the jargon, conformable).