Elementary Algebra Exam 2 Review
For Exam 2, you will need to be able to:
1. Graph a line given its equation; this includes “slanted” lines, horizontal
lines and vertical lines. 4.2–4.4
2. Graph a line given a point on the line and the slope of the line. 4.3
3. Find the x-intercept and the y-intercept of a line given an equation of the
line. 4.2
4. Find the slope of a line passing through two points on the line, or state
that the slope is undefined. 4.3
5. Find the slope of a line given the graph, or state that the slope is
undefined. 4.3
6. Find the x-intercept and the y-intercept of a line given the graph. 4.2
7. Write an equation of a line given a graph. 4.2 & 4.4
8. Write an equation of a line given the slope of the line and a point on the
line. The final answer should be in slope-intercept
form. 4.4
9. Write the equation of a line given two points on the line. The final answer
should be in slope-intercept form. 4.4
10. Write a linear equation that represents an application and use this model to
answer questions. 4.5
11. State whether an ordered pair is a solution to a system of linear equations
or not. 5.1
12. Determine whether a system has one solution, no solution, or an infinite
number of solutions, by writing each equation in slopeintercept
form and comparing the slopes and y-intercepts. 5.1
13. Solve a system of linear equations graphically. This includes systems that
have one unique solution, no solution, or an infinite
number of solutions. 5.1
14. Solve a system of linear equations by substitution. This includes systems
that have one unique solution, no solution, or an infinite
number of solutions. 5.2
15. Solve a system of linear equations by addition (elimination). This includes
systems that have one unique solution, no solution, or
an infinite number of solutions. 5.3
16. Solve “mixture” and other applications problems involving systems of linear
equations. 5.2–5.4
17. Simplify expressions using the rules of exponents, including expressions
with both positive, negative and zero exponents. 6.1
& 6.2
18. Convert from scientific notation to decimal notation. 6.3
19. Convert from decimal notation to scientific notation. 6.3
20. State the degree and the leading coefficient of a polynomial. 6.4
21. Add two polynomials by combining like-terms. 6.4
22. Subtract two polynomials by first distributing the minus sign to the
appropriate polynomial and then combining like-terms. 6.4
23. Multiply two polynomials by distributing. For two binomials this is called
“FOIL”-ing. These problems includes—but are not
limited to—expressions of the form ( a + b)2 or ( a − b)2
.
6.5
24. Divide a polynomial by a monomial. 6.6
25. Divide a trinomial by a binomial. 6.6
Exam Information
The best way to study for this exam is to actually practice, or redo, a lot of
problems from the chapter reviews, chapter tests,
worksheets, and your homework after you have finished “looking over” all of your
notes, homework, and worksheets.
There are approximately 30 problems on Exam 2. No more than two of these 30
problems are “word problems”.
You may use a 3" X 5" note card (both sides). Formulas will not be
given on the exam.
Notes
• Intercepts are points; in other words, they consist of an x-value and a
y-value. To find the x-intercept, plug in 0 for y and solve
for x; this will give you a point (?, 0). To find the y-intercept, plug in 0 for
x and solve for y; this will give you a point (0, ?).
• Slope of a line, m, may be defined as follows:
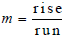 or as
or as 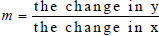 or
as
or
as 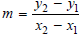
where 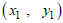 and
and 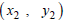 are points on the line.
are points on the line.
• Parallel lines have the same slopes. Perpendicular lines have
the slopes that are opposite reciprocals.
• A horizontal line has a slope of 0. The equation of a horizontal line
is y = " a c o n s t a n t " . For example 2y = - 4 or
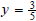 .
.
There is no x-variable present in the equation.
A vertical line has an undefined slope. The
equation of a vertical line is x = " a c o n s t a n t " . For example 2x = - 4
or
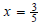 . There is no y-variable present in the
equation.
. There is no y-variable present in the
equation.
• Slope-intercept form of an equation of a line is y = mx + b where m is
the slope of the line, and (0 , b) is the y-intercept
of the line.
• Point-slope form of an equation of a line is
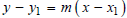 where m is the slope of the line, and
where m is the slope of the line, and
![]() is a point
is a point
on the line.
• There are three different types of solutions for a system of linear equations:
1. One solution which is the point of intersection where the two lines
cross. This is a consistent system. These two lines
have different slopes.
2. No solution. The lines are parallel, so they never intersect. This is
an inconsistent system. These two lines have the same
slope, but different y-intercepts.
3. Infinitely many solutions. The equations represent the same line. All
points on this line are solutions to the system. This
is a dependent system. These two equations have the same slope and the same
y-intercept.
• When adding or subtracting—combining like-terms—the variable part,
including the exponent, stays exactly the same,
only the coefficients are added or subtracted. Example: 2x + x → 3x
• When multiplying, the exponents on the variable part of a
factor may
change. Example: 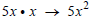
• When multiplying factors of the same base, the exponents are added. Example:
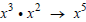
• When raising a power to a power, multiply exponents. Example:
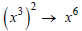
Review Problems
Show only one solution for each problem. Simplify all your answers.
Graph the equation.
Find the x-intercept and the y-intercept of the line.
4. 1 8x − 6y = 3 6
x-intercept: ( , )
y-intercept: ( , )
Find the slope of the line through the given points.
5. (−2 , − 4) and (1 , 5)
6. (3 , 1) and (3 , − 2)
Find the slope of each line or state that the slope is
undefined, and then use the graph to determine (and write down) the y-intercept
and the
x-intercept.
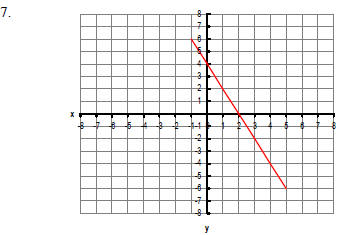 |
Slope: x-intercept: ( , ) y-intercept: ( , ) |
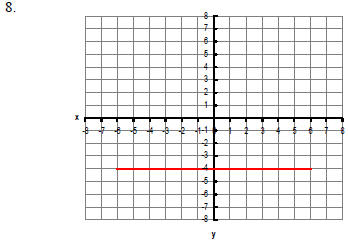 |
Slope: x-intercept: ( , ) y-intercept: ( , ) |
Graph the line described, and then write an equation for
the line.
9. The slope is –2 and the y-intercept is (0 , 3) .
10. The slope is 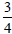 and the line contains the point (1 , − 3) .
and the line contains the point (1 , − 3) .
Find the equation of the line with the given properties. Your final answer
should be in slope-intercept form.
11. The slope is –5 and the line contains the point (0 , 3) .
12. The slope is 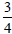 and the line contains the point (8 , − 1) .
and the line contains the point (8 , − 1) .
13. The slope is 0 and the line contains the point (− 6 , 5) .
14. Passing through the points (−2 , − 4) and (1 , 5) .
15. Passing through the points (3 , 1) and (3 , − 2) .
For problem 16, do the problem from the book.
16. Page 275 Number 72 Parts a through c
State whether the ordered pair is a solution to the system. You must show how to check if a point is a solution to a system to receive full credit.

Determine the solution to each system of equations
graphically. If the system is has one solution, find it. If the system has
no solution, state so. If the
system has infinitely many solutions, give these specific solutions. You must
show a graph of the system and state an answer to receive full credit.
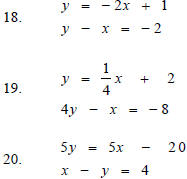
Express each equation in slope-intercept form and then
state whether the system has one exactly one solution, no solution or an
infinite number
of solutions.
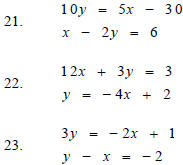
Determine the solution to each system of equations by
substitution. If the system has exactly one solution, find it, state so.
If there are infinitely
many solutions to the system, give these specific solutions. You must show
the substitution method for this system and state an answer to receive
full credit.
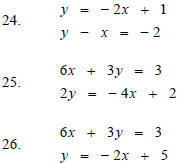
Determine the solution to each system of equations by
the addition method. If the system has exactly one solution, find it, state
so. If there are
infinitely many solutions to the system, give these specific solutions. You
must show the addition method for this system and state an answer to
receive full credit.
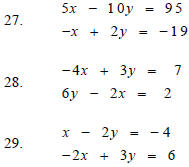
For problems 30 and 31, you must do each of the following:
a) Define any variables that you use.
b) Write a system of equations that represents the relationships in the word
problem.
c) Solve your system of equations, any way you choose.
d) Answer the question in the word problem.
30. Jerome’s experiment requires him to mix a 50% acid solution with an 80% acid
solution to create 200 milliliters of a 68% acid
solution. How much 50% acid solution and how much 80% acid solution should he
use?
31. Entering Yellowstone National Park costs $20 for a car and $15 for a
motorcycle. On a typical day, 5950 cars or motorcycles
enter and pay a total of $107, 875. How many cars and how many motorcycles enter
on a typical day?
Simplify each expression. Write your final answer with positive exponents.
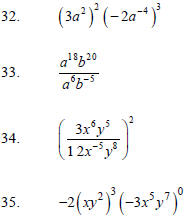
Express the number in decimal form (without exponents).
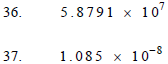
Express the number in scientific notation.
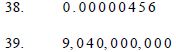
Add.
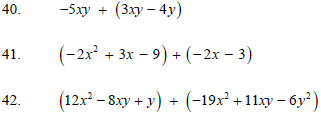
Subtract.
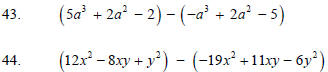
Multiply.
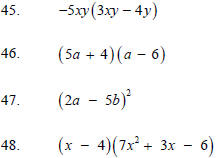
Divide.
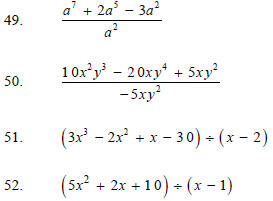
Extra Review Problems
For more practice problems, do the Chapter 4, Chapter 5 and Chapter 6 Tests in
the book. The answers are available in the back of
the book.


