NUMERICAL AND ALGEBRAIC EXPRESSIONS
In arithmetic, we use symbols such as 4, 8, 17, and π to
represent
numbers. We indicate the basic operations of addition, subtraction,
multiplication, and division by the symbols +, -, ·, and ÷, respectively. Thus
we can formulate specific numerical expressions. For example, we can
write the indicated sum of eight and four as 8 + 4.
In algebra, the concept of a variable provides the basis for
generalizing.
By using x and y to represent any number, we can use the expression
x + y to represent the indicated sum of any two numbers. The x and y in
such an expression are called variables, and the phrase x + y is called an
algebraic expression. We commonly use letters of the alphabet such as
x, y, z, and w as variables. The key idea is that they represent numbers;
therefore, as we review various operations and properties pertaining to
numbers, we are building the foundation for our study of algebra.
Many of the notational agreements made in arithmetic are extended to
algebra with a few slight modifications. The following chart summarizes the
notational agreements pertaining to the four basic operations.
| Operation | Arithmetic | Algebra | Word phrase |
| Addition | 4 + 6 | x + y | The sum of x and y |
| Subtraction | 7 - 2 | w - z | The difference of w and z |
| Multiplication | 9 · 8 | a·b, a(b), (a)b, (a)(b) or ab |
The product of a and b |
| Division | 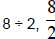 or or
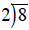 |
The quotient of c and d |
As we review arithmetic ideas and introduce algebraic
concepts, it is
convenient to use some of the basic vocabulary and symbols associated
with sets. A set is a collection of objects, and the objects are called
elements or members of the set. In arithmetic and algebra, the
elements
of a set are often numbers. To communicate about sets, we use set
braces, { }, to enclose the elements (or a description of the elements), and
we use capital letters to name sets. For example, we can represent a set
A, which consists of the vowels of the alphabet, in these ways:
A = {vowels of the alphabet} Word description, or
A = {a, e, i, o, u} List or roster description
If we write {1, 2, 3, . . .} the set begins with the
counting numbers, 1, 2, and
3. The three dots indicate that it continues in a like manner forever; there is
no last element. A set that consists of no elements is called the null set
(written 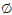 ).
).
Two sets are said to be equal if they contain exactly the same elements.
For example, {1, 2, 3} = {2, 1, 3} because both sets contain the same
elements; the order in which the elements are written doesn’t matter. The
slash mark through the equality symbol denotes “not equal to.” Thus, if A =
{1, 2, 3} and B = {1, 2, 3, 4}, we can write A ≠ B, which we read as “set A is
not equal to set B.”
Simplifying Numerical Expressions
Let us simplify some numerical expressions that involve the set of whole
numbers – that is, the set {0, 1, 2, 3,…}. Keep in mind that when we
simplify numerical expressions, the operations should be performed in the
order listed below:
Order Of Operations
1. Perform the operations inside the parentheses and brackets and
above and below each fraction bar. Start with the innermost
inclusion symbol.
2. Perform all multiplications and divisions in the order in which they
appear from left to right
3. Perform all additions and subtractions in the order in which they
appear from left to right.
EXAMPLE 1. Simplify
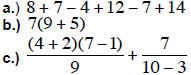
Solution:
a.)
b.)
c.)
EXAMPLE 2. Simplify
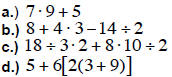
Solution:
a.)
b.)
c.)
d.)
EXERCISE 3. Work problems 1, 3, 7, 11, 15, 19 and
25 on page 8 of the
textbook.
Simplifying Algebraic Expressions
We can use the concept of a variable to generalize from numerical
expressions to algebraic expressions. Each of the following is an example
of an algebraic expression.
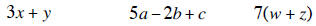
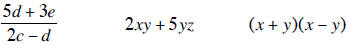
An algebraic expression takes on a numerical value
whenever each
variable in the expression is replaced by a specific number. For example, if
x is replaced by 9 and z by 4, the algebraic expression x - z becomes the
numerical expression 9 - 4, which simplifies to 5. We say that x - z has a
value of 5 when x equals 9 and z equals 4. The value of x - z, when x
equals 25 and z equals 12, is 13. The general algebraic expression x - z
has a specific value each time x and z are replaced by numbers. Consider
the next examples, which illustrate the process of finding a value of an
algebraic expression. The process is often referred to as evaluating
algebraic expressions.
EXAMPLE 4. Find the value of 3x + 2y when x is replaced with 5 and y
by 17.
Solution:
EXAMPLE 5. Find the value of 12a - 3b when a = 5 and b = 9.
Solution:
EXAMPLE 6. Evaluate 4xy + 2xz - 3yz when x = 8, y = 6 and z = 2.
Solution:
EXAMPLE 7. Evaluate 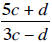 when c = 12 and d = 4.
when c = 12 and d = 4.
Solution:
EXAMPLE 8. Evaluate (2x + 5y)(3x - 2y) when x = 6 and y = 3.
Solution:
EXERCISE 9. Work problems 35, 37, 41 and 49 on
pages 8 - 9 of the
textbook.


